Step-by-Step Guide to Astrodynamics: Hohman Transfer

In this instalment we will explore the most basic method of changing orbit, Hohmann Transfer. This is a set of three maneuvers. To begin we have to leave our starting orbit, that inserts us into elliptical orbit with apogee at the same altitude as our target orbit. Once at apogee you perform a second burn to raise your perigee and achieve target orbit.

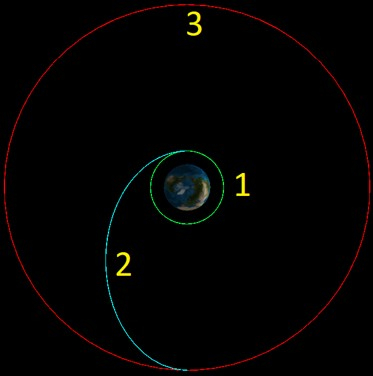
Figure 1 - Hohmann Transfer

So how do we go about this? We have two options, and we will go through both. First is an analytical method using vis-viva equation. We see that there are two maneuvers, the first one to achieve elliptical transfer trajectory and second to achieve the final circular orbit. To compute the delta-v we will be using the vis-viva equation: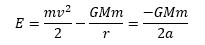

Where r is the distance to the center of the planet from your spacecraft, a is semi-major axis, G is gravitation constant and together with M which is mass of the planet they represent standard gravitational parameter μ.

When we solve the equation for velocity we get

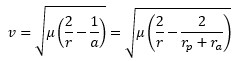Where  rp and ra are the distances to the gravitational center at periapsis and apoapsis respectively. That leads to these equations. First for velocity in the starting orbit

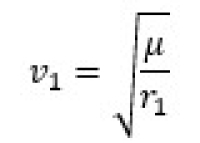
And the velocity of the elliptical transfer at periapsis

Now we need to combine it to get delta-v

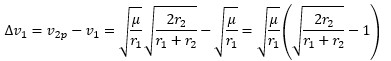
Now we need to do the same for the other maneuver, where we first need the velocity at the apogee of the elliptical transfer

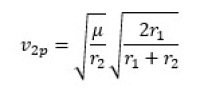
And the velocity on the final circular orbit

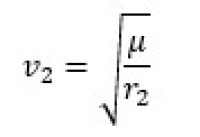
Giving us the second delta-v as

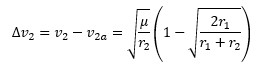
This is an awful lot of math that must be redone every time you want to change the starting or final orbit. And that is why we will now look at how to do this in GMAT. Our first step is setting up our initial orbit:

Figure 2 - Setting up initial orbit

Once that is done, we need to set up our mission sequence. First, we will set up Target for the burn that gets us to the elliptical transfer orbit, with Vary command to adjust the Δv1 to correct value. After applying the impulse burn we propagate the spacecraft to apoapsis and check the magnitude of radius, RMAG, to confirm we have achieved the value of our target orbit.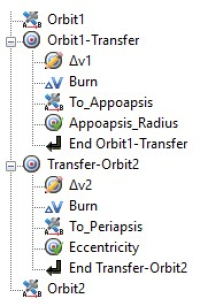

Figure 3 - Mission Sequence

We repeat the same for our maneuver to final orbit, with one difference. Our condition is aimed at achieving circular orbit, which means zero eccentricity. This way the Target command will converge quickly and accurately independently of what our desired final orbit is. This program then allows you to easily change your desired starting orbit in the spacecraft parameters and your final orbit only by adjusting desired RMAG of the first Target command.

Some of you might ask why then even mention the first part with all the equations, because it is far easier to create this short and simple simulation than deal with lengthy equations. The answer is simple, in the world of engineering simulations are powerful tools, but it is one that you first need to properly validate and make sure it truly represents what you think it does. It is good practice to be able to somehow verify that the simulation you are using is indeed giving you correct results. Now knowing what the result should be, you can verify that the GMAT does indeed give you correct answers in these simulations and therefore it is correct in similar cases too.